Dem Abstrakten Gestalt geben

Die mathematische Beschreibung einer Seifenblase

Schon Einstein, so heißt es, habe Schwierigkeiten mit der Geometrie der gekrümmten Flächen gehabt. Er mußte sie erst bei einem befreundeten Mathematiker lernen, so weiter, ehe er in der Lage war, seine spezielle Relativitätstheorie zu beschreiben. Die Tatsache, daß selbst einer der größten Physiker beinahe an der Mathematik gescheitert wäre, mag ein wenig Trost spenden, wenn man in Prof. Ulrichs Pinkalls Büro steht, und erkennen muß, daß man ganz, ganz wenig weiß - jedenfalls in Mathematik.

Ulrich Pinkall ist Sprecher des Sonderforschungsbereiches 288 ”Differentialgeometrie und Quantenphysik", in dem Mathematiker und theoretische Physiker zusammenarbeiten, um einerseits Verfahren der Mathematik in der Physik einzusetzen und andererseits Anregungen aus der theoretischen Physik für mathematische Methoden aufzugreifen. In diesem Sonderforschungsbereich, einem der wenigen in Deutschland, die in einem mathematischen Fachbereich angesiedelt sind, sind die Mathematiker die Experimentatoren. Bei ihnen geht es zunächst einmal um Grundlagenforschung, genauer gesagt um Differentialgeometrie. Das ist reine Mathematik, weit entfernt von Anwendungen. Aber vielleicht ist es gerade die Abstraktheit dieser Formeln, die es am Ende doch ermöglicht, sie in vielen Gebieten einzusetzen.

”Differentialgeometrie", erklärt Ulrich Pinkall, ”beschäftigt sich mit gekrümmten Gebilden", mit der Frage wie, und mit welchen Funktionen und Gleichungssystemen man sie beschreiben kann. Einfachstes Beispiel mag die Seifenblase sein, an der auch die Mathematiker Gefallen gefunden haben. Sie stellt eine Fläche dar, deren Krümmung überall gleich ist und die bei festem Volumen immer die kleinstmögliche Oberfläche hat. Solche Flächen, Seifenblasen eben, kann man mathematisch noch relativ leicht beschreiben, mit einer sogenannten Solitonengleichung. Mit genau solchen Gleichungen - von wegen keine Verbindung zur Anwendung - wird zum Beispiel auch die Ausbreitung von Wellen durch ein Glasfaserkabel (wie es beim Telefongespräch geschieht) oder der Verlauf von Wasserwellen beschrieben.

Die Wissenschaftler stellen Fragen an die Geometrie, darin besteht ihr Experiment, und versuchen herauszufinden, wie eine Fläche aussieht, die ihre Bedingungen erfüllt. Sie minimieren Krümmungen oder Inhalt, maximieren oder halten bestimmte Eigenschaften der Flächen konstant. Je nach den Randbedingungen, die sie vorgegeben haben, entsteht ein geometrisches Gebilde, das den Anforderungen der Mathematiker genügt. Oder wie Ulrich Pinkall sagt: ”Komplizierte Flächen beantworten einfache Fragen". Und dann gilt es, Zusammenhänge oder Gleichungen zu finden, die diese Fläche beschreiben und mathematisch korrekt zu beweisen, daß dies auch so ist.

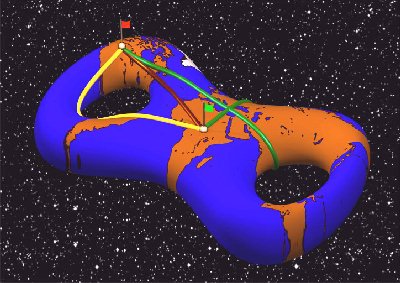
Zu den einfacheren, noch vorstellbaren Gebilden gehört der Thorus , sozusagen ein zu einem Ring zusammengelegter Gartenschlauch. Mathematisch formuliert ist das eine zusammenhängende Fläche mit einem Loch. Man kann beweisen, daß die Krümmung dieses Gebildes immer dann minimal wird, wenn das Verhältnis von Durchmesser des ”Gartenschlauchs" zu Durchmesser des Lochs einen ganz bestimmten Wert hat. Bei Flächen mit zwei Löchern gibt es nur Vermutungen, wann die Krümmung minimal wird. Ein Beweis steht noch aus.

SEIFENBLASEN UND QUANTENMECHANIK

Die Methoden, die zur Behandlung solch geometrischer Fragestellungen eingesetzt werden, haben sehr viel mit Fragen aus der mathematischen Physik zu tun. Die Raum-Zeit-Krümmung, mit der schon Einstein zu kämpfen hatte, ist nur ein Beispiel dafür. Auch Probleme der Quantenmechanik, der Quantenfeldtheorie oder der Elementarteilchenphysik lassen sich mit Gleichungen aus der Differentialgeometrie beschreiben. Und so ”hat sich erstaunlicherweise herausgestellt, daß man da viel mit anfangen kann". Auch wenn die Mathematiker nicht auf Anwendung hin gearbeitet haben, besitzen ihre Formeln doch praktische Bedeutung zur Berechnung von Schiffsrümpfen, Dachkonstruktionen und Autokarosserien oder eben in der Physik. Und da kann es dann passieren, daß komplizierte physikalische Systeme, die fernab von jeglichem Vorstellungsvermögen sind, nicht nur mathematisch beschreibbar werden, sondern auch - zumindest für den Fachmann - in den Flächen der Mathematiker eine konkrete Gestalt bekommen.

Wohl nicht zuletzt deshalb spielt die Visualisierung der geometrischen Gebilde im Sonderforschungsbereich eine große Rolle. Da es entsprechende Software nicht gab, mußte sie neu entwickelt werden. Mit aufwendigen graphischen Mitteln wurden hier, aber auch in andren, Forschungsinstituten, Videos realisiert, die einen Einblick in die Welt der Differentialgeometrie ermöglichen.

Diese sind beim Video Math Festival, das im Rahmen des International Congress of Mathematicians vom 18. - 27. August in Berlin stattfindet, und vom Sfb 288 zusammen mit dem Konrad Zuse Institut organisiert wird, zu sehen. Dort kann auch der Laie, selbst wenn er von Mathematik nichts versteht, einfach nur staunen und genießen.

Ursula Resch-Esser